Congrès APMEP[1]– 20 octobre 2018 – Bordeaux
Dans la première approche d’une figure mathématique, on ne reconnait pas spontanément des formes et des surfaces.
La reproduction de la figure ci-contre peut se faire en un
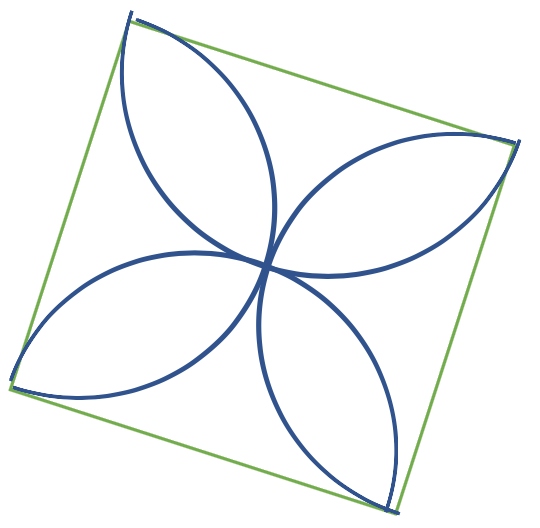 assemblage par superposition ou juxtaposition.
assemblage par superposition ou juxtaposition.
Or, ce sont deux perceptions différentes, dans la juxtaposition
on ne voit pas de cercles, et la vision ne sera pas opératoire.
Pour reproduire la figure, il faut voir les différents éléments :
carré, cercles, demi-cercles ; une déconstruction
dimensionnelle est nécessaire pour penser sa reconstruction.
Il faut analyser la figure en unités figurales, or cette vision
n’est ni immédiate ni automatique. L’enseignant est amené à
changer le regard.
Comment provoquer ce changement de regard sur les figures géométriques ? Comment passer d’un regard de formes et de surfaces à une vision des figures géométriques ?
Le langage est aussi important que la situation que l’on présente aux élèves. Or dans les manuels les problèmes de reproduction sont peu pris en compte.
Cette séquence propose une progression pour enseigner et apprendre le cercle.
Reproduire le modèle (les situations ne sont pas strictement successives, on peut passer à la 2 et/ou à la 3 sans la 1 – les expérimentations ont été menées à plusieurs niveaux des cycles 2 et 3)
Situation 1 – Les élèves ont à leur disposition les demi-cercles et pas le carré : ils juxtaposent les demi-cercles sans rapport avec la figure à reproduire.
Situation 2 – Le carré est introduit, il faut tout mettre dans le carré sans faire dépasser. Les élèves essaient différentes superpositions, ils considèrent les bords. Ils arrivent à reconstruire la figure grâce aux lignes, ils superposent et dessinent les lignes. Alors il voient des lignes qui peuvent se croiser. Ce qui est important c’est le langage comme médiateur qui permet aux élèves de conceptualiser et à l’enseignant d’institutionnaliser.
Situation 3 – Comment aller vers le réseau de lignes et de points ? Dans ce modèle qui repose sur un segment tracé, on utilise un tableau qui attribue un cout aux instruments supplémentaires que les élèves peuvent utiliser. Plus les élèves utilisent des instruments de précision, de type règle graduée, plus cela leur coute. Ils privilégient le recours au compas. Ce modèle leur impose de mener une analyse fine sur la figure-modèle en mobilisant des connaissances géométriques fondamentales grâce auxquelles ils n’ont pas besoin de mesurer.
Les élèves sont amener à formuler leurs connaissances par la verbalisation des connaissances d’action et la désignation des éléments de la figure par une communication à quelqu’un d’autre.
Conclusion – À partir de la même figure, la variation des instruments développe la conceptualisation et le langage est crucial.
- Se connecter ou s'inscrire pour poster un commentaire